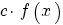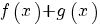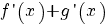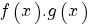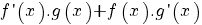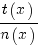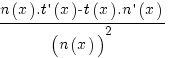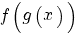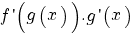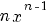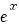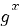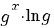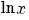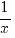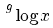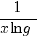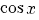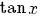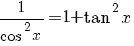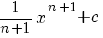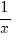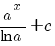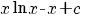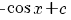VWO wiskunde formulekaart
Een overzicht van de belangrijkste wiskunde formules uit het VWO
|
Differentieren |
Integreren |
Goniometrie |
Limieten |
Vergelijkingen |
Machten en logaritmen |
Somformules voor rijen |
Differentiaal vergelijkingen |
Rekenen in driehoeken |
Rekenen in cirkels |
Parameterkrommen |
Tellen, kansrekening en kansverdelingen |
Verbanden |
terug naar bovenDifferentieren
|
|
terug naar bovenIntegreren
|
|
terug naar bovenGoniometrie
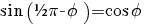 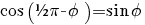 |
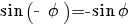 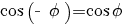 |
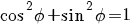 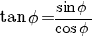 |
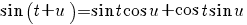 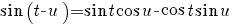   |
 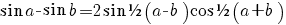 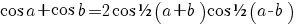 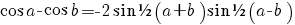 |
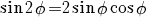  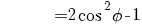  |
terug naar bovenLimieten
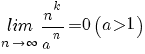 |
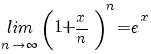 |
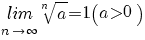 |
terug naar bovenVergelijkingen
| Vergelijking | Oplossing | Voorwaarde |
|---|---|---|
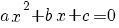 |
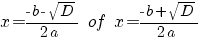 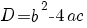 |
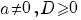 |
 |
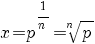 |
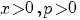 |
 |
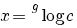 |
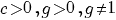 |
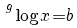 |
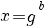 |
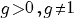 |
 |
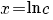 |
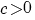 |
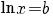 |
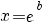 |
terug naar bovenMachten en logaritmen
De volgende regels gelden onder de voorwaarden:
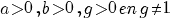
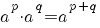 |
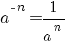 |
 |
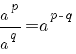 |
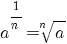 |
 |
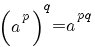 |
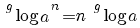 |
|
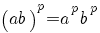 |
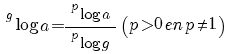 |
terug naar bovenSomformules voor rijen
Voor de rekenkundige rij 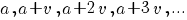 geldt
geldt
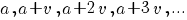
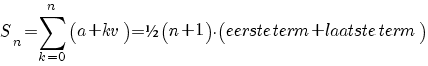
voor de meetkundige rij 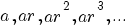 geldt
geldt
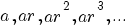
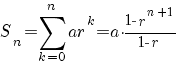
voor de som 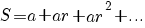 met
met 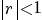 geldt
geldt
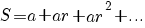
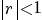

terug naar bovenDifferentiaal vergelijkingen
| Differentiaalvergelijking | Oplossing | |
|---|---|---|
| exponentiële groei | 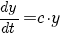 |
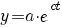 |
| begrensde groei | 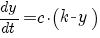 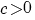 |
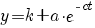 |
| logistische groei | 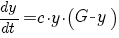 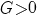 |
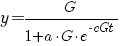 |
terug naar bovenRekenen in driehoeken
stelling van Pythagoras:
is in driehoek ABC hoek C recht, dan geldt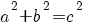
is in driehoek ABC hoek C recht, dan geldt
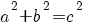
omgekeerde stelling van Pythagoras:
geldt in driehoek ABC dat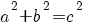 , dan is hoek C recht
, dan is hoek C recht
geldt in driehoek ABC dat
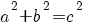
cosinusregel:
in elke driehoek ABC geldt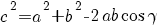
in elke driehoek ABC geldt
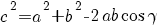
sinusregel:
in elke driehoek ABC geldt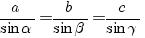
in elke driehoek ABC geldt
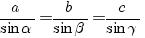
terug naar bovenRekenen in cirkels
cirkel met straal 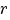 heeft een lengte van
heeft een lengte van 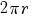 en een oppervlakte van
en een oppervlakte van 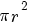
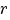
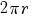
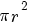
cirkelboog met straal 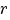 en middelpuntshoek
en middelpuntshoek  (rad) heeft lengte
(rad) heeft lengte 
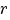


cirkelsector met straal 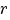 en middelpuntshoek
en middelpuntshoek  (rad) heeft oppervlakte
(rad) heeft oppervlakte 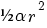
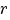

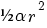
terug naar bovenParameterkrommen
Als de beweging van een punt P gegeven wordt door 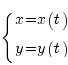
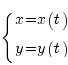
dan is de snelheid 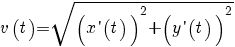
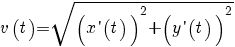
en de baanlengte op het tijdsinterval [a, b] is 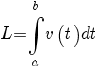
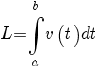
de eenparige cirkelbeweging met middelpunt (a, b), straal 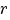 en hoeksnelheid
en hoeksnelheid 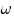
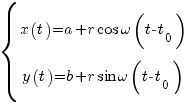
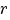
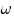
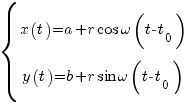
terug naar bovenTellen, kansrekening en kansverdelingen
binomium van Newton: 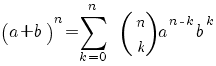
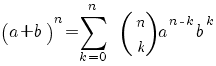
voor toevalsvariabelen X en Y geldt: 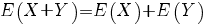
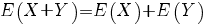
voor onafhankelijke toevalsvariabelen X en Y geldt: 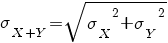
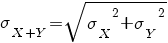
bij een serie van n onafhankelijk van elkaar herhaalde experimenten geldt
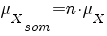 |
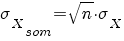 |
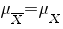 |
 |
voor de binomiaal verdeelde toevalsvariabele X met parameters n (aantal experimenten) en p (kans op succes) geldt
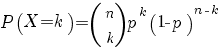
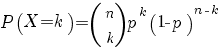
| verwachtingswaarde |
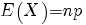 |
| variantie |
 |
| standaardafwijking |
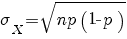 |
voor de normaal verdeelde toevalsvariabele X met gemiddelde 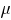 en standaardafwijking
en standaardafwijking  geldt:
geldt: 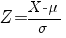 is standaard-normaal verdeeld
is standaard-normaal verdeeld 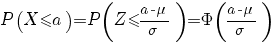
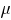

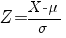
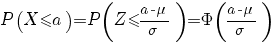
terug naar bovenVerbanden
lineair verband 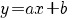 |
richtingscoefficient a |
exponentieel verband  |
beginwaarde b groeifactor g |
harmonische trilling 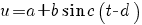 |
evenwichtsstand a amplitude |b| periode 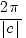 beginpunt (d, a) |
(c) Ginco.nl | Disclaimer